视频、讲义地址:吴恩达-深度学习-微专业 在线笔记
auto-encoder
优化手段-预训练(pre-training):合理初始化权重,避免出现局部最优解。
逼近identity function的意义:
- 对于监督式学习,得到的权重->特征转换,学习到数据的“特征表示”
- 对于非监督式学习,可以估计密度,排除不典型的数据(g(x)≠x)。 学习到数据的“典型表示”。
basic auto-encoder: 被分类为非监督式学习
denoising-autoencoder:输入有噪声的数据,输出无噪声的数据
PLA:percetron learning algrithm PCA:Principal Component Analysis auto-encoder和PCA求解问题的方法相似
转置卷积
- 输出计算公式
- $H_{out} = (H_{in} - 1) \times \text{stride}[0] - 2 \times \text{padding}[0] + \text{kernel_size}[0] + \text{output_padding}[0]$
- $W_{out} = (W_{in} - 1) \times \text{stride}[1] - 2 \times \text{padding}[1] + \text{kernel_size}[1] + \text{output_padding}[1]$
- 建议:
- output_padding取 stride-1,
- padding取 (kernel_size - 1)/2
- stride是卷积核每次滑动的步长
CNN
- 对于n×n image, f×f filter, padding p, stride s,输出图像的H和W是这样的:(输出图像的通道数C=filter个数。) $\left\lfloor\frac{n+2 p-f}{s}+1\right\rfloor$ × $\left\lfloor\frac{n+2 p-f}{s}+1\right\rfloor$
- 对于立方体卷积,filter的通道数必须和输入图像的通道数保持一致(比如RGB图像,通道数就是3)。对于1×1卷积,多通道图像才有意义。
- pooling池化层:分为max和average。输入输出channels一样。 输入:$H \times W \times C$ 输出:$\left\lfloor {\frac{s} + 1} \right\rfloor \times \left\lfloor {\frac{s} + 1} \right\rfloor \times C$
- fully_connected全连接层,要指定输出通道数。
- BN、激活函数,不影响尺寸。
垂直边缘检测: 构造f*f矩阵(f通常是奇数):又称filter、kernel
valid convolutions:no padding,p=0
same convolutions:输入和输出大小相同,p=(f-1)/2, stride=1(如果等于2,输出H和W都减半)
padding(填充)解决的问题:
- 图像缩小(深度网络中,我们不希望每一步得到的结果越来越小)
- 图像边缘信息丢失(边缘处的像素只被filter使用一次,而中间部分的像素被使用多次)
从数学的角度来说,神经网络中使用的“卷积”概念其实是“互相关(cross-corelation)”。 数学中的真正的“卷积”,还包括将filter双重镜像操作,有了这个操作可以保证性质结合律
(A*B)*C=A*(B*C)。在信号处理中这是个很好的性质,但是在神经网络中并不需要,所以我们只需使用“互相关”操作。
L08:随着卷积神经网络的加深,每一层输出的立方体的H和W都在减小,但是channels在增加(filter的个数)。很多超参数需要自动学习来的。
在统计层数时候,只统计有权重和可以学习的参数的层。比如,pooling就是静态属性,没有权重,只有hyperparameter且不需要学习。
L11:Why convolutions?
- 权重共享:一个特征提取器(filter)在滑动到达的图像区域都是适用的。
- 稀疏连接:每一层的输出只和少部分的输入(一个filter覆盖的区域)有关。
卷积神经网络通过权重共享、稀疏连接这两种机制,减少了参数训练、使用更小的训练集,从而避免过拟合。
对立方体做卷积:见PPT
1×1卷积
- HPF
- 一种特殊的卷积 卷积核权重不变
- 作用:放大隐写带来的影响
- 1×1 卷积核作用
- 跨通道聚合
- 降维/升维(通道数),减少参数,避免过拟合
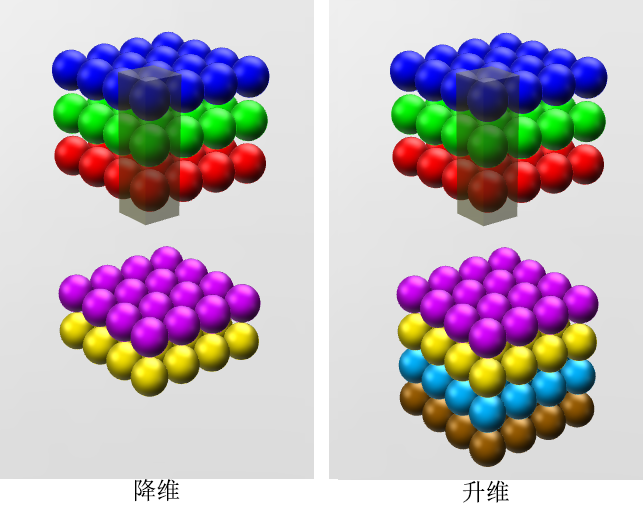
- subsample 下采样