视频、讲义地址:吴恩达-机器学习-课程
监督/非监督 学习
- 监督式:
- 输出是连续:回归问题
- 输出是离散(0/1):分类问题
- 非监督式:新闻话题检测
线性回归
- 线性回归中的代价函数,没有局部最优,只有全局最优。
- “Batch”: 每一步梯度下降使用所有的训练样本。
- 多变量线性回归的一些tricks:特征缩放
- 学习率α太小/大都会让结果很难收敛。
- 解决线性回归问题中的最小化代价函数问题:
- 梯度下降
- 正规方程组(最小二乘法):$\theta=\left(X^{T} X\right)^{-1} X^{T} y$
-
梯度下降和最小二乘法(正规方程组)对比
优缺点 梯度下降 正规方程组 优点 数据规模大也能工作 不需要学习率,不需要迭代 缺点 需要学习率,需要迭代 数据规模大时候效果不好
对率回归
- 这时候只能梯度下降来解。
- 多分类:对每个类别i都训练一个分类器$h_{i}(x)$。对于输入x,使得$h_{i}(x)$最大的i就认为是x的类别。
正则化-解决过拟合
- 减少特征数量
- 正则化(降低参数θ的值/幅度) 目标是:最小化$J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]$
神经网络表示
- 二分类:1个输出单元 多分类:k个输出单元(对于k个类别)
- 反向传播:为了方便计算梯度下降中的导数项(derivatives)。在忽略正则化项的情况下,我们认为$\frac{\partial }{\partial \theta _{ij}^{(l)}}J(\theta ) = a_j^{(l)}\delta _{\rm{i}}^{(l + 1)}$(详情见lecture 9)
- 梯度检验:验证自己写的backprop代码没有bug。检查无误之后一定要关掉梯度检验(它太慢了)。
- 如果权重全部初始化为0,结果就是每一次迭代以后得到的权重都是相等的(尽管它们不为0了),所以需要随机初始化。
- 总结
- 输入单元个数:数据特征的维度
- 输出单元个数:类别的个数
训练步骤:
- 初始化
- 前向传播计算$h_{\theta}(x)$
- 计算代价函数J(θ)
- 后向传播计算偏导数项
- 梯度检验,验证后向传播代码是否正确。(检验完毕关闭梯度检验!)
- 使用后向传播、梯度下降等方法,达到min J(θ)的目标
应用机器学习的建议
- 为什么非要是验证集而不是测试集?
- 测试集是为了测试模型的泛化性能。如果用测试集来进行超参的选择,那么这个模型将会很拟合这个测试集,导致测试集的存在失去了它自身的意义—泛化。因此,我们设置了验证集来完成这个工作。
- 人工调参(超参)是根据验证集上的效果来进行的。
- 解决high variance-过拟合:
- 减少特征维度/数量d
- 增加训练example数量
- 增大正则化参数-lamda
- 解决high bias-欠拟合:
- 增加特征维度/数量d
- 增加polynomial特征
- 减小正则化参数-lamda
支持向量机
从logistic regression说起。
- 两个算法的loss
- logistic regression的最小化目标loss:(h(x)是sigmoid函数) $min_{\theta} \frac{1}{m}[\sum_{i=1}^{m} y^{(i)}(-log h_{\theta}(x^{(i)}))+(1-y^{(i)})(-log (1-h_{\theta}(x^{(i)}))]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}$
- SVM的最小化loss:(cost1、cost0是分段函数,是上面2个log项的近似,计算更加高效)
- 两个算法的决策边界:
- logistic regression:如果h(x;θ)≥0.5,即θx≥0,则y=1;如果h(x;θ)<0.5,即θx<0,则y=0。(做决策时候不用h(x),计算loss时候用)
- SVM:如果θx≥1,则y=1;如果θx≤-1,则y=0。(做决策、计算loss都不用h(x)了)
- 核函数similarity:解决线性不可分的问题
- m个样本$(x^{(1)}, y^{(1)}),(x^{(2)}, y^{(2)}), ……,(x^{(m)}, y^{(m)})$,每个样本有m个特征$f^{(i)}=[f_{1}^{(i)}, f_{2}^{(i)}, ……, f_{m}^{(i)}]^{T}$,选择m个landmark $l^{(1)}=x^{(1)}, l^{(2)}=x^{(2)}, ……, l^{(m)}=x^{(m)}$。
- 对于某个样本$x^{(i)}$,它的特征$f^{(i)}$中每一项含义是: $f_{1}^{(i)}= similarity (x^{(i)}, l^{(1)})$ $f_{2}^{(i)}= similarity (x^{(i)}, l^{(2)})$ $\cdots \cdots$ $f_{m}^{(i)}=similarity(x^{(i)}, l^{(m)})$
- 核-SVM-最小化目标loss
- 决策边界:如果 $\theta^{T} f \geq 0$,则y=1,否则y=0
- 根据特征维度n、样本数量m的不同,logistic regression和SVM有各自不同的应用场景。
K-means algorithm
- 伪代码
randomly initialize K cluster centroids μ1,μ2...μK ∈ R repeat{ for i=1 to m $c^{(i)}$ = index(from 1 to K)of cluster centroid closest to $x^{(i)}$ for k=1 to K $μ_{k}$ = average(mean)of points assigned to cluster k } - k的选择:根据后续具体目标来定。比如T恤尺码划分:S、M、L和XS、S、M、L、XL。
降维
- 动机:数据压缩(减少硬盘存储、加快学习速度)、可视化
- 主成分分析(PCA)算法:n维->k维
- 伪代码
Σ=(1/m)*X'*X; [U,S,V]=SVD(Σ); Ureduce=U(:,1:k); z = Ureduce'*x; - 重构x
x_approx = Ureduce*z; - 选择最小的k,使得x和x_approx之间的差别最小。
- 注意:PCA不是prevent overfitting的方式。
异常检测
- 算法-密度估计
- 对于全体样本,第i个样本$x^{(i)}$的第j个维度特征的概率分布是$p(x_{j}^{(i)} ; \mu_{j},\sigma_{j}^{2})$,i ~ [1,m],j ~ [1,n]。对于参数$\mu_{1}, \dots, \mu_{n}, \sigma_{1}^{2}, ……, \sigma_{n}^{2}$,计算如下: $\begin{aligned} \mu_{j} &=\frac{1}{m} \sum_{i=1}^{m} x_{j}^{(i)} \ \sigma_{j}^{2} &=\frac{1}{m} \sum_{i=1}^{m}(x_{j}^{(i)}-\mu_{j})^{2} \end{aligned}$
-
第i个样本$x^{(i)}$的所有维度特征概率分布$p(x^{(i)})$由$p(x_{j}^{(i)} ; \mu_{j},\sigma_{j}^{2})$累乘得到。
- 对于一个新的样本x,p(x)计算方法如下。 $p(x)=\prod_{j=1}^{n} p(x_{j} ; \mu_{j}, \sigma_{j}^{2})=\prod_{j=1}^{n} \frac{1}{\sqrt{2 \pi} \sigma_{j}} \exp (-\frac{(x_{j}-\mu_{j})^{2}}{2 \sigma_{j}^{2}})$
- 如果$p(x)<\epsilon$,则判断x是异常点。(使用CV来选择$\epsilon$)
- 样本选择
- training set:正常点(y=0)
- CV/test:多数正常点(y=0),少数异常点(y=1)
- Anomaly Detection vs. Supervised Learning
- 样本类别:AD中正类样本少(y=1,异常点)负类样本多,SL中正/负类样本都很多。
- 预测效果
- AD:异常点有很多类型,未来遇到的异常点可能与我们已经见过的异常都不同,算法学习起来很困难。
- SL:未来遇到的positive examples和训练集已有的样本很像,预测较准确。
learning with large datasets
- 训练集90个,验证集10个,Batch_size=5(为了配合CPU/GPU内存,一般是2的N次方),epoch=3, 1个epoch时期等于用训练集中全部样本训练一次。
- 一个iteration等于从训练集中取batch_size个样本训练一次(这里iteration=(90*3) / 5)。
梯度下降优化算法
-
Batch gradient descent:每次iteration,使用所有m个example
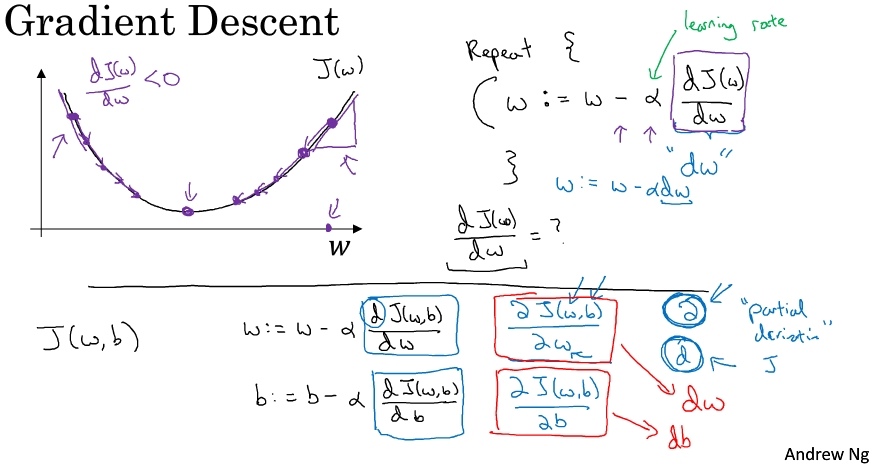

-
stochastic gradient descent:每次iteration,使用1个example

- mini-batch gradient descent:每次iteration,使用batch_size个example

-
以上3种方法收敛情况

- 指数加权平均–>动量梯度下降

- RMSprop
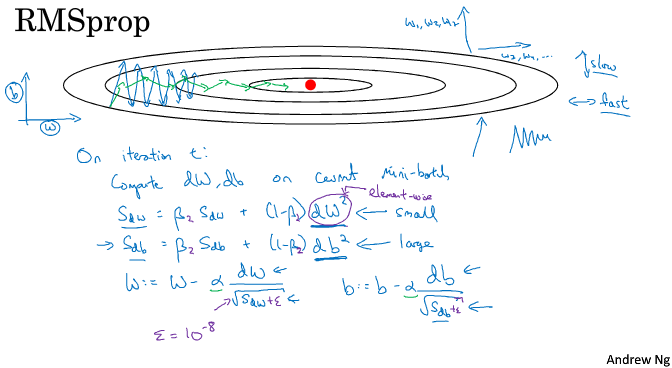
- Adam
