一,几何视角:最小二乘法LSE
- 假设有数据集D={(x1,y1), (x2,y2), …, (xN,yN)}。
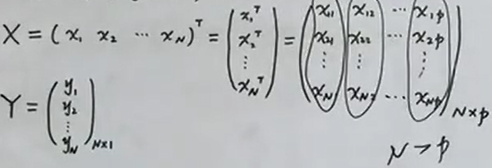
- 定义
- 最小二乘估计简称为LSE
- 线性回归假设是$ y=f(w)=w^{T}x$。
-
损失函数$ L(w)= \sum_{i=1}^{N} w^{T}x_{i} - y_{i} ^{2} $
- 由$ \hat w = arg \min_{w} L(w) $ 👉解得 $ \hat w = (X^{T}X)^{-1} X^{T}Y $
- 几何意义上的两种理解
- 希望L(w)最小,误差分散到N个样本上。(数据集里
横着圈起来的地方,依次是x1,…,xN。对应的是直角坐标系里的横坐标)
- 希望L(w)最小,误差分散到p个维度上。(数据集里
竖着圈起来的地方,依次是X1,…,Xp。对应的是p维空间)- 模型可以写成$f(w)=w^{T}x = Xβ=f(β) $,f(β)是x1,…xp的某种组合。
- 假设N个样本X张成⼀个p维空间平面P(满秩情况),我们想在P里面找到距离Y最近的一条线f(β),f(β)就是Y到P的投影。于是Y到平面的距离(虚线法向量)与f(β)垂直:$ X^{T}(Y- X \beta)=0 $ 👉 $ \beta=(X^{T}X)^{-1} X^{T}Y $
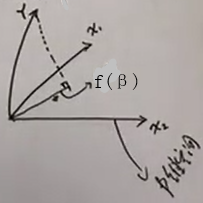
- 希望L(w)最小,误差分散到N个样本上。(数据集里
二,概率视角:MLE和LSE的关系
-
假设数据里有噪声
- $ε \sim N(0,σ^{2})$,
- $ y=f(w)+ε$, $f(w)=w^{T}x$。
-
所以,$ y x;w \sim N(w^{T}x, σ^{2}) $
- MLE做法:
-
log-likelihood是$ L(w)= log \prod_{i=1}{N} P(y_{i} x_{i};w) $, - 所以$ \hat w=arg \max_{w}L(w)
=arg \max_{w} -\frac{1}{2σ^{2}}(y_{i}-w^{T}x_{i})^{2}
=arg \min_{w}(y_{i}-w^{T}x_{i})^{2} $ - 可见,MLE推出来的$ \hat w$形式,和最小二乘法估计的一样。
-
- 结论
- 最小二乘估计,隐含的假设是,数据里噪声满足0均值的高斯分布。
- 所以,当噪声ε~Guassian时,MLE←→最小二乘估计。
三,频率角度:regularized LSE
- 回顾线性回归的loss-function,$ \hat w $的表达式
-
损失函数$ L(w)= \sum_{i=1}^{N} w^{T}x_{i} - y_{i} ^{2} $ - $ \hat w = (X^{T}X)^{-1} X^{T}Y $
-
- 为什么引入正则化:
- N是样本数量,p是每个样本维度,正常情况下N»p;
- 但是实际情况很可能是,我们样本不够多,或者p太大。
- 后果
- 数学方面:那么
X^{T}X就不可逆了。 - 现象方面:造成
过拟合
- 数学方面:那么
- 避免过拟合方法
- 加数据
- 降维:特征提取(PCA)、特征选择
- 正则化:约束w,加惩罚项P(w)
- loss= L(w) + λP(w)
- P(w)有两种
-
L1:Lasso,$P(w)= w _{1}$ -
L2:Ridge Regression(岭回归),$P(w)= w ^{2}_{1}= w^{T}w$ - L2最为常见,又称作权值衰减。
-
- 正则化框架-以Ridge Regression为例
- 使用L2作为惩罚项,带入loss-function里得到J(w),求解$ \hat w $看它长什么样子。
-
$ J(w)= \sum_{i=1}^{N} w^{T}x_{i}-y_{i} ^{2} + λw^{T}w $ - $ \hat w= arg \min_{w} J(w)
= (X^{T}X+ λI)^{-1}X^{T}Y $ - 其中,
X^{T}X+ λI一定是可逆的。 - 这么一来,我们既解决了
可逆计算问题,又解决了过拟合问题。
四,贝叶斯角度:regularized LSE和MAP的关系
- 回顾
- 最小二乘估计←→MLE(noise ε ~ Guassian)
- 正则化框架
- $ J(w)=L(w)+λP(w) $,其中L(w)是损失,P(w)是惩罚项。
- $ \hat w= arg \min_{w}J(w) $
- Ridge Regression中,令$P(w)=w^{T}w$,得到
加正则之后的最小二乘估计(regularized LSE)形式。详见👆
- 在噪声服从Guassian的情况下,考虑惩罚项。现在,从贝叶斯角度来看
加正则之后的最小二乘估计。- 假设$ w \sim N(0, σ^{2}_{0}) $
-
$ p(w y)= \frac{P(y w)P(w)}{p(y)} $ -
MAP: $ \hat w= arg \max{w} p(w y) \=arg \max_{w} p(y w)p(w) $。其中, p(y|w)和p(w)的求法如下: -
由$ y x;w \sim N(w^{T}x, σ^{2}) $可以得到 p(y|w)的表示形式; - 由$ w \sim N(0, σ^{2}_{0}) $可以得到
p(w)的表示形式。 - 二者相乘,代入MAP得
-
$ \hat w_{MAP}=arg \min_{w} \sum{i=1}^{N}(y_{i}-w^{T}x_{i})^{2}+ \frac{σ²}{σ_{0}²} w {2}^2 $。其中,前者是loss,后者是L2惩罚项,$\frac{σ²}{σ{0}²}$可以看作λ。 -
我们发现,这个表达式,刚好符合岭回归的loss定义$ J(w)= \sum_{i=1}^{N} w^{T}x_{i}-y_{i} ^{2} + λw^{T}w $。
- 结论
- 没有正则时候,
- LSE ←→ MLE(noise ε ~ Guassian)
- 以加L2正则之后的LSE(岭回归)为例,从频率角度、贝叶斯角度,来看待正则化
- regularized LSE ←→ MAP(noise和prior都服从Guassian分布)
- 没有正则时候,