线性回归

假设有数据集D={(x1,y1), (x2,y2), …, (xN,yN)}。
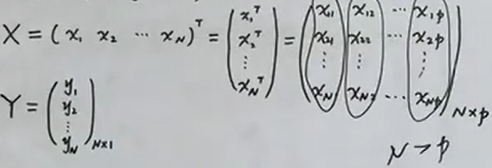
定义
- 最小二乘估计简称为LSE
- 线性回归假设是$ y=f(w)=w^{T}x$。
- 损失函数$ L(w)= \sum_{i=1}^{N} w^{T}x_{i} - y_{i} ^{2} $
由$ \hat w = arg \min_{w} L(w) $ 👉解得 $ \hat w = (X^{T}X)^{-1} X^{T}Y $
几何意义上的两种理解
- 希望L(w)最小，误差分散到N个样本上。(数据集里横着圈起来的地方，依次是x1,…,xN。对应的是直角坐标系里的横坐标)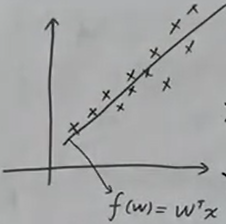
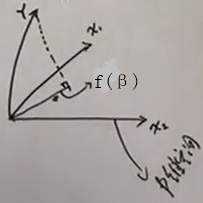
- 希望L(w)最小，误差分散到p个维度上。(数据集里竖着圈起来的地方，依次是X1,…,Xp。对应的是p维空间)
  - 模型可以写成$f(w)=w^{T}x = Xβ=f(β) $，f(β)是x1,…xp的某种组合。
  - 假设N个样本X张成⼀个p维空间平面P(满秩情况)，我们想在P里面找到距离Y最近的一条线f(β)，f(β)就是Y到P的投影。于是Y到平面的距离（虚线法向量）与f(β)垂直：$ X^{T}(Y- X \beta)=0 $ 👉 $ \beta=(X^{T}X)^{-1} X^{T}Y $

假设数据里有噪声
- $ε \sim N(0,σ^{2})$，
- $ y=f(w)+ε$， $f(w)=w^{T}x$。
- 所以，$ y x;w \sim N(w^{T}x, σ^{2}) $
MLE做法：
- log-likelihood是$ L(w)= log \prod_{i=1}{N} P(y_{i} x_{i};w) $，
- 所以$ \hat w=arg \max_{w}L(w)
  =arg \max_{w} -\frac{1}{2σ^{2}}(y_{i}-w^{T}x_{i})^{2}
  =arg \min_{w}(y_{i}-w^{T}x_{i})^{2} $
- 可见，MLE推出来的$ \hat w$形式，和最小二乘法估计的一样。
结论
- 最小二乘估计，隐含的假设是，数据里噪声满足0均值的高斯分布。
- 所以，当噪声ε~Guassian时，MLE←→最小二乘估计。

回顾线性回归的loss-function，$ \hat w $的表达式
- 损失函数$ L(w)= \sum_{i=1}^{N} w^{T}x_{i} - y_{i} ^{2} $
- $ \hat w = (X^{T}X)^{-1} X^{T}Y $
为什么引入正则化：
- N是样本数量，p是每个样本维度，正常情况下N»p；
- 但是实际情况很可能是，我们样本不够多，或者p太大。
- 后果
  - 数学方面：那么X^{T}X就不可逆了。
  - 现象方面：造成过拟合

避免过拟合方法

P(w)有两种

L1：Lasso，$P(w)=

_{1}$

L2：Ridge Regression(岭回归)，$P(w)=

^{2}_{1}= w^{T}w$

在噪声服从Guassian的情况下，考虑惩罚项。现在，从贝叶斯角度来看加正则之后的最小二乘估计。

MAP: $ \hat w= arg \max{w} p(w y) \=arg \max_{w} p(y w)p(w) $。其中，p(y|w)和p(w)的求法如下：

$ \hat w_{MAP}=arg \min_{w} \sum{i=1}^{N}(y_{i}-w^{T}x_{i})^{2}+ \frac{σ²}{σ_{0}²}

{2}^2 $。其中，前者是loss，后者是L2惩罚项，$\frac{σ²}{σ{0}²}$可以看作λ。

我们发现，这个表达式，刚好符合岭回归的loss定义$ J(w)= \sum_{i=1}^{N}

w^{T}x_{i}-y_{i}

^{2} + λw^{T}w $。

结论
- 没有正则时候，
  - LSE ←→ MLE（noise ε ~ Guassian）
- 以加L2正则之后的LSE(岭回归)为例，从频率角度、贝叶斯角度，来看待正则化
  - regularized LSE ←→ MAP（noise和prior都服从Guassian分布）

LSE,MLE; regularized LSE; 频率/贝叶斯角度