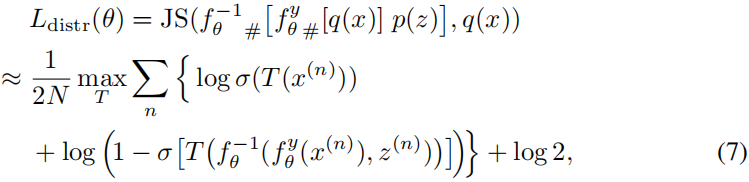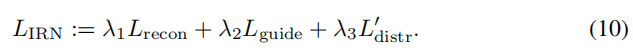概述
出处
- 题目：Invertible Image Rescaling
- 用可逆网络完成图像缩放任务
- 单位
- Peking University
- Microsoft Research Asia
- Toronto University
- 源码地址
- https://github.com/pkuxmq/Invertible-Image-Rescaling
动机、方法、实验效果
- https://github.com/pkuxmq/Invertible-Image-Rescaling
- 问题背景
- 为了适应各种显示屏/节省存储成本/带宽，高分辨率图像通常会缩小。
- 同时，为了恢复原始分辨率，还要保证可以放大回去。
- 目标：缩小图像的放大重建 任务。
- 现有的图像缩放方法存在以下问题
- 由于高频信息的丢失，逆过程(放大)存在不适定问题。
- 怎样从低分辨率图像中恢复细节，是一大挑战。
- 本文怎样解决这个问题？
- 利用可逆缩放网络（IRN），对缩小/放大过程进行建模：（卖点1，首创）
- 可逆双射变换，大大减轻图像放大的不适定性。
- IRN 可以生成 视觉质量良好 的低分辨率图像。
- 同时在缩放过程中，使用
潜在变量(指定某种分布)来捕获高频(丢失信息)的分布。（卖点2，参数减少） - 这样，将 潜在变量与低分辨率图像反向传递通过网络，就可得到 高分辨率图像。
- 利用可逆缩放网络（IRN），对缩小/放大过程进行建模：（卖点1，首创）
- 本文方法效果如何？
- 对于 缩小图像的放大重建 任务，
- 在定量/定性评估方面，本文模型比现有方法有了显着改进。（卖点3）
前置知识：不适定性
- Encoder-Decoder 框架
- 对降采样（压缩）和升采样（重建）进行建模。
- 然而，上述框架存在一个严重的问题：
- 最后一步从低维信息中还原原始图像的过程，是一个典型的不适定 (ill-posed) 问题。
- 举例说明：4像素点图像-降采样
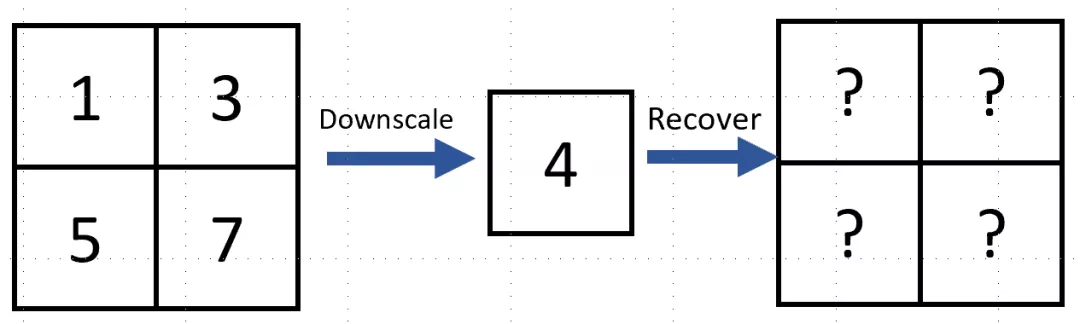
- 上图有4个像素，值分别为1,3,5,7。
- 假设对原图进行双线性插值降采样（Bilinear Interpolation），得到像素值为4的低分辨率图片。
- 那么，如何从这一个像素还原出原图？
- 很难求解。因为有无数多种4个像素取值的组合都可以得到同样一张低分辨率的图片。
- 在降采样的过程中存在着不可逆的信息丢失, 以至于仅从剩余的不完全信息中无法很好地还原回原图。这就是不适定问题。
- 对于图像缩放任务中的不适定问题，现有的解决方法：
- 超分辨率-CNN，尝试从大量的数据中强行学习低分辨率到高分辨率的映射关系；
- 使用encoder对原图降采样，同时使用decoder还原图片，二者进行联合训练（jointly training）。
- 但是，以上这些方法都没有从本质上解决不适定问题，效果也不尽如人意。
方法
-
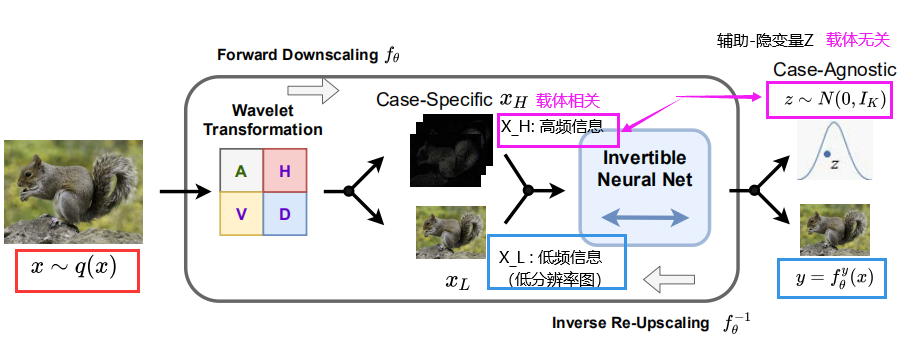
- 文章提出的网络叫做IRN。主要思想是，引入 辅助 潜在变量Z（服从某种分布），和 高频信息（丢失信息） 之间 做可逆映射。（如图所示,有一种条件flow的意味）。
- 用INN有两个好处。一个是可逆，一个是
去相关作用。（或者称作ICA？）去相关就是，把两个有相关性的信息 X_H 和 X_L，转换为彼此独立的Z和y。类似于 ICA（independent component analysis，独立主成分分析），把一串有相关性的信号，分解为彼此独立的信号。举个例子，语音分离任务里的鸡尾酒会问题。- 最早的flow模型NICE，题目里就包含了ICA思想。把现实世界里的复杂未知分布X（X的每个分量可能是彼此相关的），转换为一个简单分布Z（Z的每个维度分量 是彼此独立的）。
- 对于上图的描述
- 高频信息(由Z生成) + 低分辨率图像 -> 高分辨率图像
- 小波变换 将高分辨率图像x分解为低频分量x_L和高频分量x_H。
- Z 是样本 无关的，但是训练时候是 样本 相关 的。
-
与 样本 无关 的z，即z~p(Z)，而不是 样本相关 的z~p(z y)。 - 但是训练时候，Z 还是用到了 样本 相关的 高频信息 统计信息。
- 结构上，小波变换可逆，InvBlock使用了flow的块。二者都是可逆的，所以整个IRN也是可逆的。
损失 三个
- 保证-IRN生成的-低分辨率图像质量：LR Guidance
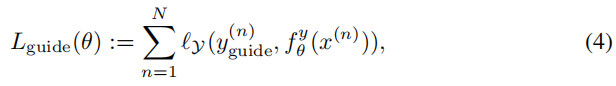
- 其中：
- $X^(n)$ 是高清原图
- $y^(n)_{guide}$ 是 原图 经过 Bicubic（双三线性插值）之后的结果
- $ f^y_{theta}(x^(n)) $ 是整个IRN网络的输出的 低分辨率图
- $L_y$ 是 L1或L2 loss
- 保证-恢复高清图像-质量：HR Reconstruction
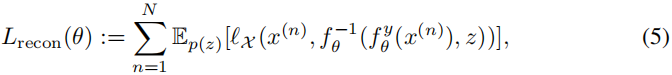
- 其中，$L_X$ 表示 original image 和 reconstructed one 之间的差距。（推测也是L1或L2 loss）
- 保证-恢复高清图像-和-原图-同分布：Distribution Matching
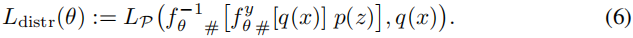
- 其中，
- $L_P$ 是 JS divergence，
- 高清原图-分布 x ~ q(x)
- 低分辨率图+隐变量 联合分布
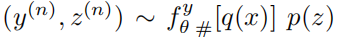，y(n)和z(n)独立 
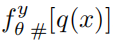表示，IRN输出的 低分辨率图 $ f^y_{theta}(x) $ 的分布
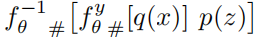表示 重构-高清图像 的分布
- 以上1~3就是训练目标（损失）的组成。
- （1）是为了保证低分辨率图的质量。（2，3）都是为了让 恢复高清图像 更真实，更接近原图。
- （3）是IRN的核心思想。作用有：
- 1让恢复图像更真实（捕捉原图-分布），
- 2使得z和y彼此独立。（GAN和flow都无法做到这些）
- 最小化（3）有两大困难：
- 1 维度高
- 2 密度函数-未知
- 所以，最小化（3）借鉴了GAN的思路（但是和GAN不同）,利用JS divergence。
- 由于 上式 训练 不稳定，所以，用下面交叉熵（弱化的，预训练的。但是更加稳定。）取代：
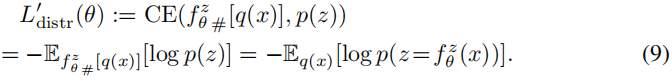
总 损失
- 公式
- 说明：
- 由于不知道fyθ＃[q（x）] p（z）的密度函数，只有p（z）的已知。
- 因此，IRN没有使用像flow那样的MLE损失。
