机器学习系列笔记根据课程整理而来。
频率派VS贝叶斯
- 问题背景:假设有个样本,每个样本都是p维向量。其中每个观测都是由
p(x|θ)⽣成的。 - 频率派
- 认为θ是常量,\(θ_{MLE} = arg \max_{θ} log{ P ({x \\| θ}) }\)
- 贝叶斯派
- 认为θ是变量,θ~P(θ)先验分布
-
由贝叶斯定理,有$$ {P(θ X)} = \frac{P()P(θ)}{P(X)} \sim P(X,θ) \sim likelihood×prior $$ - 注意,这里P(X)涉及积分很难求👉为了便于计算,假设变量之间有
条件独立关系,👉这种关系用图表示👉概率图模型。 - 概率图中,边表示条件概率,节点表示变量。而
神经网络是函数逼近器,节点表示计算组件。
- 注意,这里P(X)涉及积分很难求👉为了便于计算,假设变量之间有
- 贝叶斯后验估计\(θ_{MAP}= arg \max_{θ} {P({θ \\| X})}\)
- θ估计出来以后,就可以做贝叶斯预测了
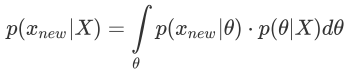
- 由此发展出来的两大理论板块
- 频率派👉优化问题👉模型($f(w)=w^{T}x$)、策略(设计loss)、算法(SGD, EM),对应的理论是
统计机器学习。 - 贝叶斯👉求积分👉MCMC等,对应的理论是
概率图模型。
- 频率派👉优化问题👉模型($f(w)=w^{T}x$)、策略(设计loss)、算法(SGD, EM),对应的理论是
多维高斯分布
- 一维的就不写了,高维的PDF(probability distribution formula)如下
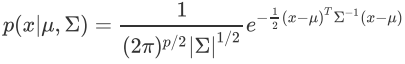
- 局限性有二:
- 一是为了估计μ和Σ需要训练参数太多👉假设Σ是对⻆矩阵(Factor Analysis),或者在各向同性假设中假设其对⻆线上的元素都相同(p-PCA)
- 二是有时不能假设是同分布的👉GMM
- 把高维的X分成Xa, Xb两部分:
- 根据⾼斯分布的定理
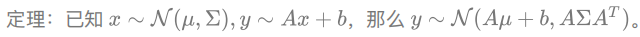 ,
, P(Xa),P(Xb | Xa);P(Xb),P(Xa | Xb)是有解析解的。 - 所以,利用这四个量,这个问题也可以求出来了
.png)
- 根据⾼斯分布的定理