线性分类

一、背景

1. 线性回归中，引入非线性的几个方面
   • 属性：特征转换（多项式回归），比如$ f=w_{1}x_{1}^{2} + w_{2}x_{2}^{2} +w_{3}x_{1}x_{2}$
   • 全局：激活函数非线性 → 线性分类
   • 系数：感知机、神经网络（初始值不同，结果不同）
   • 局部：线性样条回归（输入空间分段，每一段都是非线性）、决策树
   • 数据未加工：降维PCA
2. 线性回归、线性分类：关系
   • 贝叶斯派👉概率图模型
   • 频率派👉统计机器学习👉线性回归👉激活函数、降维👉线性分类
3. 线性分类：两个方面
   • 硬分类
     • 线性判别分析(LDA, Linear Discriminant Analysis)，由fisher发明
     • 感知机
   • 软分类
     • 生成式：高斯判别分析GDA（名字有歧义）、朴素贝叶斯
       • 通过贝叶斯MAP，不是求解P(Y|X)具体值，而是比较P(Y|X)大小，从而确定，给定X时Y属于什么类别。（预测问题）
     • 判别式：逻辑回归 Logistic Regression（名字有歧义）
       • 直接建模P(Y|X)，比如MLE

二、感知机

1. 模型如下。(思想：错误驱动。)
   • $ f(x)= sign(w^{T}x) $
   • $ sign(a)= +1, a≥0 $
   • $ sign(a)= -1, a<0 $
2. 策略
   • 定义
     • D={被错误分类的样本}
     • $ 样本集= {(x_{i}, y_{i})}_{i=1}^{N} $
     • 损失L(w)是被错误分类的点的个数
   • $ L(w)= \sum_{i=1}^{N} I {y_{i}w^{T}x_{i}<0 } $
   • 但是，L(w)不是连续函数，不可导。所以👇
   • $ L(w)= \sum_{x_{i}∈D} - y_{i}w^{T}x_{i} $
   • L(w)对w的梯度就是$\triangle_{w}= -y_{i}x_{i}$
3. 算法：SGD
   • $ w^{t+1}= w^{t} -\lambda \triangle_{w} $

三、线性判别分析（fisher）

1. 定义
   • $ X=(x_{1}^{T},x_{2}^{T},…,x_{N}^{T})_{N×p} $
   • $ Y=(y_{1},y_{2},…,y_{N})_{N×1} $
   • $ 样本集= {(x_{i}, y_{i})}{i=1}^{N} $，其中$ x{i}∈R^{p}, y_{i}∈{ c_{1}= +1, c_{2}= -1 } $

   • $ x_{c1}={ x_{i}

     y_{i}=+1 }, x_{c2}={ x_{i}

     y_{i}=-1 } $

   • $

     x_{c1}

     =N_{1},

     x_{c2}

     =N_{2}, N_{1}+N_{2}=N $

2. 投影/降维思想：类内小（方差足够小），类间大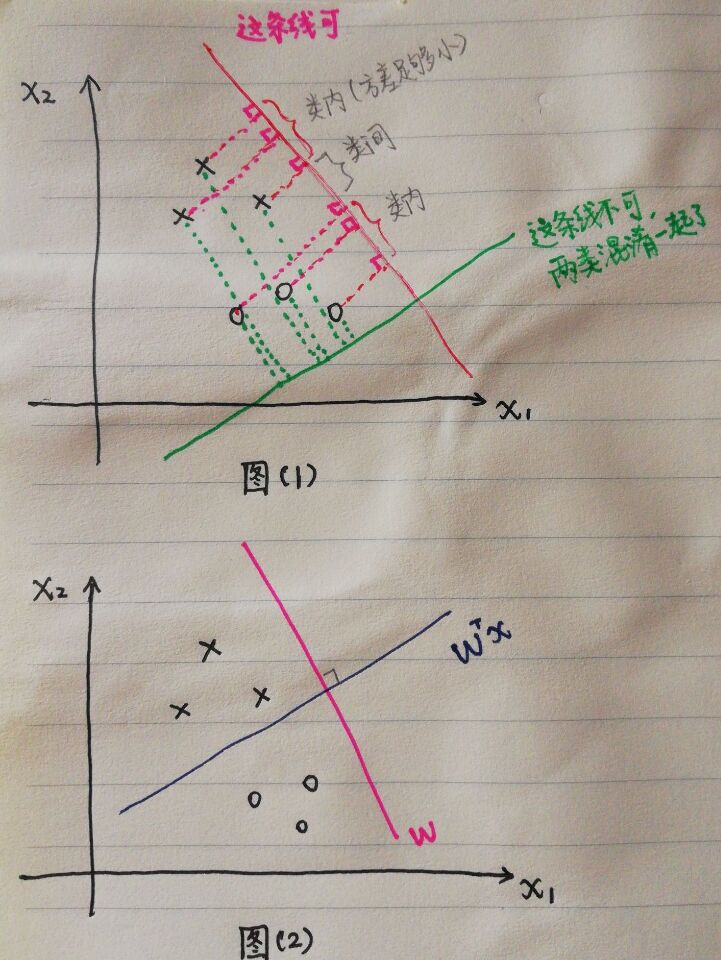
   • 
   • 找到合适的投影方向（下图(1)中，红色/绿色的线），使得同类的点，在此方向上的投影接近，不同类的点，投影距离远。

   • 为了表达类内/类间差距，引入投影概念。图(2)中，$x_i$在w上的投影=$w^{T}x_{i},

     w

     =1$

3. 类内/类间差距
   • 对于类别C1里的所有点，
     • 计算$x_i$在w上的投影的均值：$ \bar Z_{1}=\frac{1}{N_{1}}\sum_{i=1}^{N_{1}} w^{T}x_{i} $，
     • 计算方差$ S_1=\frac{1}{N_{1}}\sum_{i=1}^{N_{1}} (w^{T}x_{i}- \bar Z_{1})^2 $
   • 对于类别C2里的所有点，同理得到$ \bar Z_{2}, S_2 $
   • 类内差距：$ S_1+S_2 $
   • 类间差距：$ (\bar Z_1-\bar Z_2)^2 $
4. 目标函数J(w)

   • 定义$\bar X_{c1}$是类别C1里的所有点$x_i$的均值,$S_{c1}$是方差；对于类别C2同理得到$\bar X_{c2}$和$S_{c2}$。

   • $ J(w)= \frac{ (\bar Z_1-\bar Z_2)^2 }{S_1+S_2} = \frac{w^T (\bar X_{c1}-\bar X_{c2})^2 w}{w^T (S_{c1}+S_{c2}) w} $

   • $ \hat w= arg \max_w J(w) $

五、逻辑回归 Logistic Regression

1. 前置知识
   • $ 样本集= {(x_{i}, y_{i})}_{i=1}^{N} $
   • sigmoid function：
2. 建模P(Y|X)（likelihood），用MLE求w \(\hat w=arg \max_w logP(Y|X)\) \(\hat w=arg \max_w log \prod_{i=1}^{N} P(y_i|x_i)\) \(\hat w=arg \max_w \sum_{i=1}^{N} logP(y_i|x_i)\) \(\hat w=arg \max_w \sum_{i=1}^{N} (y_i log p_1 + (1-y_i)log p_0 )\)
3. Σ里面的内容，其实是- Cross Entropy。
   • 所以，MLE(max likelihood)👉min Cross_Entropy

六、高斯判别分析（GDA,Gaussian Discriminant Analysis）

1. 回顾
   • $ 样本集= {(x_{i}, y_{i})}{i=1}^{N} $，其中$ x{i}∈R^{p}, y_{i}∈{ 0,1 } $
   • 贝叶斯MAP： P(y|x)~P(x|y)P(y),即posterior ~ likelihood*prior

   • 生成模型里，用MAP对P(y|x)建模：$ \hat y= arg \max_{y∈{0，1}} P(y

     x) \sim arg \max_y P(y)P(x

     y) $

2. MAP👉GDA
   • 假设prior y~Bernoulli(α)
     • p(y=1)= α
     • p(y=0)= 1-α
     • $ p(y)=α^y (1-α)^{1-y} $
   • 假设likelihood x|y服从方差相同，均值不同的高斯分布
   • x|y=1 ~ N(μ_1,Σ), 记作$p_1$
   • x|y=0 ~ N(μ_0,Σ), 记作$p_0$

   • $ P(x

     y)=p_1^y p_0^{1-y} $

3. 求解GDA：目标函数

   • $ L(θ)=log \prod_{i=1}^{N} P(x_i,y_i)
     = \sum_{i=1}^{N} [log p(x_i|y_i) + log p(y_i)] $，代入即可

   • $ θ=(μ_1,μ_2,Σ,α) $
   • $ \hat θ= arg \min_θ L(θ) $
4. 求解GDA：参数估计
   • $ \hat α= \frac{N_1}{N} $
   • $ \hat μ_1= \frac{ \sum_{i=1}^{N} y_i x_i }{N_1} $
   • $ \hat Σ= \frac{1}{N}(N_1 S_1 + N_2 S_2) $，其中，$N_1、N_2$分别是属于类别y=1或者y=0的样本个数，$S_1、S_2$分别是两种类别的样本方差。

九、朴素贝叶斯

1. 思想
   • 最简单的概率图（有向图）
   • 朴素（条件独立性）假设
     • 动机：简化运算
     • 给定Y的类别，X的各个属性（维度）是独立的。（图中，一共有P个维度）

     • $ P(X

       Y)= \prod{j=1}^{p}p(x_j

       y) $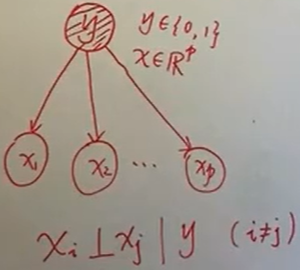

     • 
2. 数据和目的
   • $ 样本集= {(x_{i}, y_{i})}{i=1}^{N} $，其中$ x{i}∈R^{p}, y_{i}∈{ 0,1 } $
   • 目的是预测问题：给定x，类别y是0/1？
3. 公式
   • $ \hat y= arg \max_{y∈{0,1}} P(y|x)
     = arg \max_y \frac{P(x,y)}{P(x)}
     = arg \max_y \frac{P(y)P(x|y)}{P(x)}
     \propto \max_y P(y)P(x|y) $
4. P(y), P(x|y)怎么求？
   • 先验P(y)的假设
     • 0/1二分类：y ~ Bernoulli分布
     • 多分类：y ~ Categorial分布
   • P(x|y)：两个假设

     • 条件独立假设：$ P(x

       y)= \prod{j=1}^{p}p(x_j

       y) $

     • 服从分布假设
       • X离散(一般情况)：$x_j \sim Categorial分布 $
       • X连续：$x_j \sim N(μ_j, σ_j^2) $，即每个维度满足正态分布
   • P(y), P(x|y)的分布假设出来了，那么MLE就可以求得。
5. 补充
   • Bernoulli👉二项分布
     • 一次实验（0/1两种选择）👉N次实验
   • Categorial👉多项式分布
     • 一次实验（K种选择）👉N次实验

• Previous
  线性回归
• Next
  降维：PCA(Principal component analysis)